排序指的是将一组对象按照某种逻辑重新排列的过程,在计算机早期,大约30%的时间都用在排序上,今天这个比例降低了,这得益于高效的排序算法。排序有大量的应用场景,它往往是解决问题的第一步,它很基础但很重要,比如快速排序就被誉为20世纪科学和工程领域10大算法之一。排序如此有用的一个重要原因是在一个有序数组中查找一个元素比在一个无序数组中查找要简单的多。今天我们就来研究一下。
本文从排序的经典算法开始分析,依次介绍交换排序、插入排序、希尔排序三个初级排序算法,然后分析使用分治思想设计的高级排序算法:归并排序和快速排序以及堆排序,最后研究字符串排序方法。
排序基础
排序的要求
稳定性要求
需要明确排序后的重复数据是否需要保持原数据的相对顺序,比如两份数据相等的情况下,原来排在前面的数据A排序后是否仍然排在前边。我们将会分析的插入排序和归并排序是稳定排序,但很多不是,比如选择排序、希尔排序、快速排序和堆排序。
原地排序
当排序数据规模较大时,排序对空间复杂度有一定要求,如果排序是否能过做到原地排序,不需要额外的存储空间。
外排序 or 内排序
我们是否需要对完整数据从小到大排序,还是只是需要对部分数据排序,比如只需要获取TOP10数据?
性能要求
待排序数据本身杂乱无序还是只是一小部分数据无需,数据本身的特点对排序算法的选择很重要,输入本身决定了算法的性能,比如小数据排序初级排序算法就够了。
排序的成本模型
在研究排序算法时,我们需要计算比较和交换的数量。对于不交换元素的算法,我们需要计算访问数组的次数。
比较排序算法
我们在本节研究经典的选择排序、插入排序、希尔排序、归并排序、快速排序和堆排序。排序算法研究我们先从最暴力的初级排序开始,循序渐进探索更高级时间复杂度更小的排序算法,这也是正确的打开方式,大部分算法问题的解并非一开始就最优的,大部分都是不是在设计出第一版(当然,首先必须保证正确),然后探索优化的可能。
初级排序算法
选择排序
选择排序是能够想到的暴力排序解法之一,其基本思想是:
首先,找到数组中最小的那个,然后和数组第一个元素交换。
接着,找到数组接下来第二小的元素,然后和第二个元素交换。
以此类推,直到完成最后一个元素的排序。
其实很明显的感知到,这是一个笨方法,算法并不优秀,存在大量的重复比较。但是不管怎样,如果没有想到更好的解法,笨方法也是方法啊,我们先实现一下,代码如下。
public static void sort(Comparable[] a) {
for (int i = 0; i < a.length; i++) {
int min = i;
for (int j = i + 1; j < a.length; j++)
if (less(a[j], a[min])) min = j;
exch(a, i, min);
}
}
private static boolean less(Comparable a, Comparable b) {
return a.compareTo(b) < 0;
}
private static void exch(Object[] a, int i, int j) {
Object swap = a[i];
a[i] = a[j];
a[j] = swap;
}
可以看出,对于长度为N的数组,选择排序需要大约 N^2 / 2 次比较,需要N次交换。
选择排序算法和数组原来是否有序无关,也就是说如果数组本来就有序,仍然需要上述这么多次比较和交换。但和我们要求的其他算法相比,选择排序交换的次数是最少的,只需要N次交换。
插入排序
插入排序也是比较简单的排序算法,想法何打牌时按顺序整理手中的牌是一样的:将每张牌插入到其他已经有序的牌中。
为了给待插入的牌腾位子,我们需要在插入前向右移动一位。
插入排序的顺序取决于输入元素的初始顺序,比如对于一个有序或接近有序的数组进行插入排序会比乱序数组快很多。因此,插入排序应用比较多的场景是非随机数组。插入排序 代码如下:
public static void sort(Comparable[] a) {
for (int i = 1; i < a.length; i++) {
for (int j = i; j > 0 && less(a[j], a[j - 1]); j--)
exch(a, j, j - 1);
}
}
从代码实现我们也能看出对于部分有序的数组,插入排序十分高效。而对于随机无序无重复主键的数组,插入排序和选择排序的运行时间是平方级别的,两者之比应该是一个较小的常数,一般插入排序比选择排序快一倍。
希尔排序
希尔排序是基于插入排序跟快速的排序算法,目的是改善插入排序的问题:对于大规模乱序数组插入排序很慢,原因是它只会交换相邻的元素,因此元素只能一点一点地从数组的一端移到另一端,如果最小的元素在数组的尽头,要将它移到最左端需要移动N-1次。
希尔排序改进了插入排序,通过交换不相邻的元素对数组的局部进行排序,最终用插入排序将局部的数组排序。希尔排序的思想是使任意间隔h的元素都是有序的,这样的数组被称为h有序数组。如下图所示。
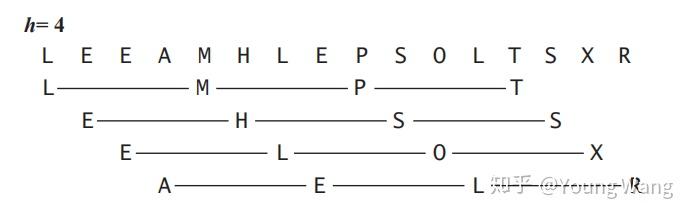
希尔排序的高效在于:它权衡了子数组的规模和有序性。通过将数组分割成多个子数组,减少了排序的规模,且子数组排序之后,子数组部分有序。
下面是算法的实现。
public static void sort(Comparable[] a) {
int h = 1;
while (h < a.length / 3) h = 3 * h + 1;
while (h >= 1) {
// 将数据变成h有序
for (int i = h; i < a.length; i++) {
for (int j = i; j >= h && less(a[j], a[j - h]); j -= h)
exch(a, j, j - h);
}
h = h / 3;
}
}
上述实现我们选择的递增公式为h = 3 * h + 1,即递增序列为1,4,13,40,121,364…,递增序列的选择会影响算法的性能,有比3*h+1更佳的递增序列,更加优秀的递增序列有待发现,这里我们不做进一步分析。
希尔排序和插入排序以及选择排序相比,它要快得多,并且数组越大,优势越大。通过提升速度来解决朴素方法无法解决的问题正是研究算法设计和性能的主要原因。
希尔排序实现代码比其他更高级的排序算法更简单,且不需要额外的内存空间,如果手头并没有现成的排序函数可以调用,实现一个希尔排序是一个不错的选择。
归并排序
归并排序是理解分治思想很好的例子。归并即将两个有序数组归并成一个更大的数组,归并排序的思想是先递归地将数组分成两半分别排序,然后将结果归并起来。如下图所示。

归并排序的优点是对于任何规模的待排序数组N,所需的时间和NlogN成正比,归并排序的主要缺点是它需要额外空间和N成正比。
归并排序算法实现可根据自顶向下或自底向上实现。自顶向下归并排序使用了分治思想,如果它能够将两个子数组排序,那么它就能够通过归并两个子数组将整个数组排序。
递归法自顶向下实现。
public class Merge {
private static Comparable[] aux;
public static void sort(Comparable[] a) {
aux = new Comparable[a.length];
sort(a, 0, length - 1);
}
// 将数组a[lo..hi]排序
private static void sort(Comparable[] a, int lo, int hi) {
if (hi <= lo) return;
int mid = lo + (hi - lo) / 2;
sort(a, lo, mid);
sort(a, mid + 1, hi);
merge(a, low, mid, hi);
}
// 将a[lo..mid] 和 a[mid+1..hi]归并
private static void merge(Comparable[] a, int low, int mid, int hi) {
int i = lo, j = mid + 1;
for (int k = lo; k <= hi; k++)
aux[k] = a[k];
for (int k = lo; k <= hi; k++) {
if (i > mid) a[k] = aux[j++];
else if (j > hi) a[k] = aux[i++];
else if (less(aux[j], aux[i])) a[k] = aux[j++];
else a[k] = aux[i++];
}
}
}
我们已经提到对于任意规模的数组N,归并排序都能做到时间复杂度为O(N) = NlgN,但如果处理的数据规模很小,则使用递归归并排序继续缩小问题规模就显得没有必要,反而会导致方法调用过于频繁,插入排序很可能在小数组排序上比归并排序更快,已经有人做过归并排序优化,使用插入排序处理小规模的子数组(一般长度小于15),可以将归并排序的时间缩短10%~15% 。
迭代法自底向上归并实现。
public class MergeBU {
private static Comparable[] aux;
public static void sort (Comparable[] a) {
int N = a.length;
aux = new Comparable[N];
for (int size =1; size < N; size = size + size) {
for (int lo = 0; lo < N - size; lo += size + size)
merge(a, lo, lo + size - 1, Math.min(lo + size + size - 1, N - 1));
}
}
}
迭代法可以有效减少由于递归导致的栈空间的使用。
快速排序
快速排序可能是应用最广泛的排序算法,它有太多优点:
- 实现简单。
- 适用于不同输入数据,且一般情况比其他排序算法快很多。
- 它是原地排序。
将长度为N的数组排序所需的时间和NlgN成正比。既是原地排序,同时又具有良好的排序性能,排序算法实在是太优秀了。
快速排序也是一种分治的排序算法,它也是将一个数组分成两个子数组,然后将两部分独立排序。这样看,和归并排序基本一致,事实上快速排序和归并排序是互补的:归并排序将两个数组分别排序,并将有序子数组归并以将整个数组排序;而快速排序将整个数组排序的方式则是当两个数组都有序时整个数组自然有序。快速排序切分排序过程如下所示。

切分示意图如下所示。
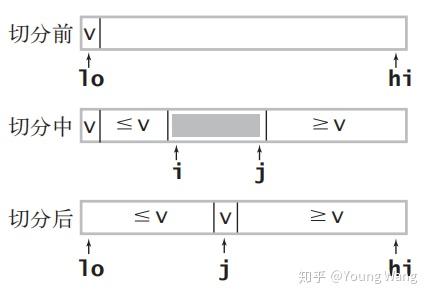
快排的实现代码如下。
public class Quick {
public static void sort(Comparable[] a) {
StadRandom.shuffle(a);
sort(a, 0, a.length - 1);
}
private static void sort(Comparable[] a, int lo, int hi) {
if (hi <= lo) return;
int j = partition(a, lo, hi);
sort(a, lo, j - 1);
sort(a, j + 1, hi);
}
// 将数组切分成a[lo..j - 1],a[j],a[j + 1..hi]
private static int partition(Comparable[] a, int lo, int hi) {
int i = lo, j = hi + 1;
Comparable v = a[lo];
while (true) {
while (less(a[++i], v)) if (i == hi) break;
while (less(v, a[--j])) if (j == lo) break;
if (i >= j) break;
exch(a, i, j);
}
exch(a, lo, j);
return j;
}
}
从上述代码实现可以看到我们一开始打乱的数组,这是为了让数组保持随机,数组越随机,选择的切分元素越能保证切分元素两边的子数组规模接近一致。快速排序在最好情况下正好可以保证数组对半分。需要比较的次数Cn ~ NlgN。和归并排序、希尔排序相比,排序排序在内循环中需要移动的数据很少,这也是快排算法优秀的两外一个原因之一。
算法的实现上需要注意的点很多,比如:需要保证数组访问不越界,递归可终止等等。
优先队列和堆排序
上述算法都需要对整个数组进行排序,但存在大量的应用,我们只需要获取给定规模的数据很小一部分的排序结果,比如top10的数组,如果排序的数据规模巨大,比如超过了单台内存的极限,这时上面谈到的所有算法就无能为力了,这时候我们需要考虑外排序,比如堆排序,而堆排序使用到的正是优先队列这种数据结构(也叫二叉堆)。再讨论堆排序前有必要优先队列API。
优先队列API
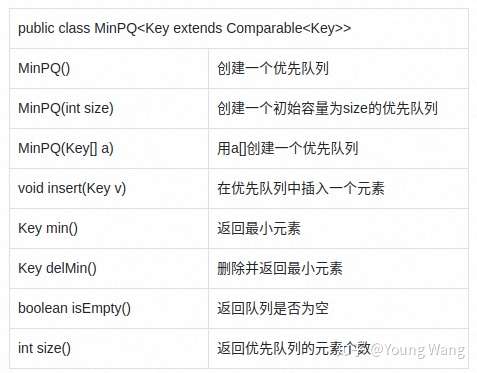
调用示例
从N个输入中找到交易最大的M个交易,从大到小打印。
public static void printTopM(Transaction[] transactions, int m) {
MinPQ<Transaction> pq = new MinPQ<>(m + 1);
for (Transaction transaction : transactions) {
pq.insert(tranction);
if (pq.size > m) pq.delMin();
}
Stack<Transaction> stack = new Stack<>();
while (!pq.isEmpty()) stack.push(pq.delMin());
for (Transaction t : stack) System.out.println(t);
}
优先队列实现
优先队列一般用二叉堆来实现,当一棵二叉堆结点都大于等于它的子结点时,被称为堆有序。二叉堆是一组能够用堆有序的完全二叉树排序的元素,在数组中按照层次存储。如下图所示。

public class MaxPQ<Key extends Comparable<Key>> {
private Key[] pq;
private int size = 0;
public MaxPQ(int maxN) {
pq = (Key[])new Comparable[maxN + 1];
}
public boolean isEmpty() {
return size == 0;
}
public void insert(Key v) {
pa[++size] = v;
swim(size); // 上浮操作,恢复堆的有序性,调整堆为最大堆;
}
public Key delMax() {
Key max = pq[1];
exch(1, size--);
pq[size + 1] = null;
sink(1); // 下层,恢复堆的有序性
return max;
}
// 上浮
private void swim(int k) {
while (k > 1 && less(k / 2, k)) {
exch(k / 2, k);
k = k / 2;
}
}
// 下沉
private void sink(int k) {
while (2 * k <= size) {
int j = 2 * k;
if (j < size && less(j, j + 1)) j++;
if (!less(k, j)) break;
exch(k, j);
k = j;
}
}
}
以下是插入元素时上浮操作和删除最大元素的下沉操作示意图。

堆排序
通过上述基于堆的优先队列的分析,我们可以基于优先队列API实现堆排序:将待排序的所有元素查找最小元素的优先队列,然后再重复调用删除最小元素的操作将它们按顺序删除。
堆排序算法实现如下。
public static void sort(Comparable[] pq) {
int n = pq.length;
// heapify phase
for (int k = n/2; k >= 1; k--)
sink(pq, k, n);
// sortdown phase
int k = n;
while (k > 1) {
exch(pq, 1, k--);
sink(pq, 1, k);
}
}
堆排序分2个阶段:堆化阶段和下沉排序阶段。如下面这个例子。

2.5.排序算法性能对比

比较排序应用
问题:荷兰国旗问题
给定一个包含红色、白色和蓝色,一共 n 个元素的数组,**原地**对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
此题中,我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
注意:
不能使用代码库中的排序函数来解决这道题。
示例:
输入: [2,0,2,1,1,0]
输出: [0,0,1,1,2,2]
进阶:
- 一个直观的解决方案是使用计数排序的两趟扫描算法。
- 首先,迭代计算出0、1 和 2 元素的个数,然后按照0、1、2的排序,重写当前数组。
- 你能想出一个仅使用常数空间的一趟扫描算法吗?
解:
应用三指针分别指向0的右侧,2的左侧和从左到右顺序遍历的当前指针

解:
public void sortColors(int[] nums) {
if (nums.length == 0) return;
int p0 = 0, p2 = nums.length - 1, curr = 0;
while (curr <= p2) {
if (nums[curr] == 0) {
int temp = nums[p0]; // p0可能指向0或1
nums[p0++] = nums[curr];
nums[curr++] = temp;
}
else if (nums[curr] == 2) {
int temp = nums[p2];
nums[p2--] = nums[curr];
nums[curr] = temp;
}
else curr++;
}
}
问题:计算前K个高频词汇
给定一个非空的整数数组,返回其中出现频率前 *k* 高的元素。
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
示例 2:
输入: nums = [1], k = 1
输出: [1]
解:
使用优先队列
public int[] topKFrequent(int[] nums, int k) {
Map<Integer, Integer> map = new HashMap<>();
for (int num : nums) map.put(num, map.getOrDefault(num, 0) + 1);
PriorityQueue<Integer> pq = new PriorityQueue<>((a, b) -> map.get(a) - map.get(b));
for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
Integer num = entry.getKey();
Integer frequency = entry.getValue();
if (pq.size() < k) pq.add(num);
else if (frequency > map.get(pq.peek())) {
pq.remove();
pq.add(num);
}
}
int[] res = new int[k];
for (int i = 0; i < k; i++) res[i] = pq.remove();
return res;
}
基于计数排序的字符串排序算法
人类书面交流主要是通过字符串进行的,因此,目前大部分应用软件都是基于字符串处理。我们已经知道排序是很多应用问题解决的第一步,但应用领域基于字符串排序,比如按照ABCD…26个英文字母顺序排序,而非存数字排序的可能性更大,因此,研究字符串排序就变得很实用了。
键索引计数排序,突破了比较排序NlgN的限制,属于线性时间排序。之所以能突破是因为他的原理和我们在前面分析的比较算法不一样,它不是基于比较,且对输入有一定要求,输入是由一个范围的整数(或一定范围的字符编码)构成。
字母表
说起字符串,就要说到字符串编码,不同编码所选取的字符串范围是不同的,不同编码的字符范围我们用字母表表示,字母表需要提供如下API:


下面我们将学习两类字符串排序方法:低位优先字符串排序(LSD)和高位优先字符串排序(MSD)。如果我们把一个字符串(字符编码EXTENDED_ASCII)看做一个256进制的数字,低位优先字符串排序就是从右向左检查键中的字符,反过来,高位优先字符串排序就是从左往右检查键中字符。
低位优先字符串排序适用于键的长度相等的字符串排序应用,高位优先字符串排序不用检查所有的输入就能够完成排序,高位优先级排序和快速排序类似。
键索引计数法
键索引计数法是适合小整数键的简单排序方法,键索引计数方法本身就很实用,同时,它也是我们后面需要分析的低位优先排序和高位优先排序的基础。简单理解就是按分组占坑,然后以此填入,如下图所示是键索引计数法阶段分类。笔者私底下把键索引计数法叫位置计数法,即计算每个键下的起始位置。

键索引计数需要经过4个步骤:
- 频率统计。
- 将频率转换成索引,即数组a中每个分组在数组中的起始位置。
- 数据分类。
- 回写。
为了进一步说明键索引原理,我们举例说明。
老师在统计学生分数时有这种需求,学生被分成若干组,标号为1,2,3…,现在需要给学生按分组分类,要达到的效果如下图所示。

我们来分析一下键索引计数是如何解的。
设数组a[]表示原始输入,value是一个对象,包含学生名字和分组编码,第i个数据的分组标号通过a[i].key()获取。
a.频率统计
键就是分组号,我们用r来表示所有分组号,统计分组号的频率我们需要初始化一个数组count[r + 1],count[0]始终是0,统计代码如下:
for (int i = 0; i < N; i++)
count(a[i].key() + 1)++;
统计结果如下所示:

b.统计频率转换成索引
即计数每个分组坑位的起始位置。
for (int r = 0; r < R; r++)
count[r + 1] += count[r];

c.数据分组
for (int i = 0; i < N; i++)
aux[count[a[i].key()]++] = a[i]

d.回写
即将辅助数组拷贝回原数组,这样就完了按键分组排序的工作。
完整代码如下所示。
public void keyIndexSort(String[] a) {
int N = a.length;
String[] aux = new String[N];
int[] count = new int[R + 1];
for (int i = 0; i < N; i++)
count[a[i].key() + 1] ++;
for (int r = 0; r < R; r++)
count[r + 1] += count[r];
for (int i = 0; i < N; i++)
aux[count[a[i].key()++]] = a[i];
for (int i = 0; i < N; i++)
a[i] = aux[i];
}
计数排序是一种非基于比较的排序算法,键索引计数对小整数非常有用的排序方法,它的意义在于它突破了比较算法NlogN排序算法运行时间下限的限制,对于需要排N个键在0到R-1之间的整数的元素需要访问数组11N+4R+1次。空间复杂度和时间复杂度均为O(N+R)线性时间复杂度,其中R是整数的范围。
低位优先的字符串排序
低位优先的字符串排序算法能够稳定地将定长字符串排序。假设定长字符串长度为W,其原理是从低位开始,从低位到高,以每一位为键进行键索引计数排序,经过W次排序后最终得到定长字符串的排序结果。如下图所示。

假设前提条件是使用扩展ASCII码,即字母表总共有256个字符编码,代码实现如下。
public class LSD {
public static void sort(String[] a, int W) {
int N = a.length;
int R = 256;
String[] aux = new String[R + 1];
for (int d = W - 1; d >= 0; d--) {
int[] count = new int[R + 1];
for (int i = 0; i < N; i++)
count[a[i].charAt(d) + 1]++; // 计算频率
for (int r = 0; i < R; r++)
count[r + 1] += count[r]; // 计算分组起始位置
for (int i = 0; i < N; i++)
aux[count[a[i].charAt(d)]++] = a[i]; // 排序
for (int i = 0; i < N; i++)
a[i] = aux[i]; // 回写
}
}
}
对于典型应用R远大于N,因此低位优先字符串排序总运行时间与WN成正比。
我们可以使用地位优先字符串排序算法完成对一副扑克牌排序的排序。
高位优先的字符串排序
上一节我们分析了低位优先字符串排序,那如果字符串长度不是定长的,如果完成一个通用的字符串排序呢?
要实现一个通用字符串排序,我们应该考虑从左向右遍历所有字符,我们知道,以a开头的字符串应该排在以b开头的字符串的前面。这种从左到右的排序方法叫高位优先的字符串排序(MSD)。
和快速排序一样,高位优先字符串排序将数组切分为能够独立排序的子数组来完成排序任务,也很自然的想到通过递归来实现排序算法。如下图所示。

如下,是使用高位优先排序的排序结果。

算法实现如下。
public class MSD {
private int R = 256;
private final int M = 15; // 小数组切换阈值
private String[] aux;
private int charAt(String s, int d) {
return d < s.length() ? s.charAt(d) : -1;
}
public void sort(String[] a) {
aux = new String[a.length];
sort(a, 0, a.length - 1, 0);
}
// 以第d个字符为键对a[lo]到a[hi]排序
private void sort(String[] a, int lo, int hi, int d) {
if (hi <= lo + M) {
Insertion.sort(a, lo, hi, d);
return;
}
int[] count = new int[R + 2];
for (int i = lo; i <= hi; i++)
count[charAt(a[i], d) + 2]++;
for (int r = 0; r < R + 1; r++)
count[r + 1] += count[r];
for (int i = lo; i <= hi; i++)
aux[count[charAt(a[i], d) + 1]++] = a[i];
for (int i = lo; i <= hi; i++)
a[i] = aux[i - lo];
// 递归的以每个字符为键进行排序
for(intr r = 0; r < R; r++)
sort(a, lo + count[r], lo + count[r + 1] - 1, d + 1);
}
}
5.桶排序
和计数排序一样,桶排序也是线性时间排序,同样,它对输入也有要求,输入是随机产生,元素均匀随机的分布。
桶排序核心思想就是将要排序的数据分到几个有序的桶里,每个桶分别进行排序,然后把每个桶里的数据按照顺序依次取出,组成新的序列,该序列就是排好序的序列。
桶排序性能分析如下:
- 时间复杂度接近O(N),所以说桶排序是线性时间排序。
- 空间复杂度:桶排序中,需要创建M个桶的额外空间,以及N个元素的额外空间,所以桶排序的空间复杂度为 O(N+M)。
- 桶排序的稳定性由桶内的排序算法决定,如果桶内的排序是选择快速排序,那么桶排序是不稳定的.
总结
本文较全面的分析了常见的比较排序算法和线性非比较排序算法。从最原始暴力的交换排序算法说起,接着分析了插入排序和希尔排序,高级的用于处理更大规模的使用到分治思想的比较排序算法有归并排序和快速排序以及基于堆数据结果的堆排序。最后分析在两种线性排序算法:键索引计数排序和桶排序结束本文。希望对大家有所帮助。
The end.
转载请注明来源,否则严禁转载。原文链接